
This would quickly defeat the purpose of hashing. Name than it would be to simply do a basic sequential or binary searchĪs described earlier. If the hashįunction is too complex, then it becomes more work to compute the slot The dominant part of the storage and search process. That the hash function has to be efficient so that it does not become You may be able to think of a number of additional ways to compute hash Hashing a String Using Ordinal Values with The illustration below shows one possible way to use the The position of the character as a weight. Will always be given the same hash value. It is interesting to note that when using this hash function, anagrams The_sum = sum (ord (char ) for char in astring ) return the_sum % tablesize Returns the hash value in the range from 0 to tablesize - 1. We can then take these three ordinal values, add them up, and use theīelow is a function called hash that takes a string and a table size and The word “cat” can be thought of as a sequence of ordinal We can also create hash functions for character-based items such as

The table below shows items under both the remainder By extracting the middle twoĭigits, 93, and performing the remainder step, we get 5 ( 9 3 % 1 1 93\ \%\ 11 9 3 % 1 1). This is referred to as the load factor, and is commonlyĭenoted by λ = n u m b e r o f i t e m s t a b l e s i z e \lambda = \frac = 1,936 4 4 2 = 1, 9 3 6. The hash table at the designated position as shown in the illustration below. Once the hash values have been computed, we can insert each item into (modulo arithmetic) will typically be present in some form in all hashįunctions, since the result must be in the range of slot names. ( h ( i t e m ) = i t e m % 1 1 h(item)=item \% 11 h ( i t e m ) = i t e m % 1 1). Table size, returning the remainder as its hash value To as the “remainder method,” simply takes an item and divides it by the Our first hash function, sometimes referred Assume that we have the set of integer itemsĥ4, 26, 93, 17, 77, and 31. The hash function will takeĪny item in the collection and return an integer in the range of slot The mapping between an item and the slot where that item belongs in the Other words, there are m slots in the table, named 0 through 10. The illustration below shows a hash table of size m = 1 1 m=11 m = 1 1.

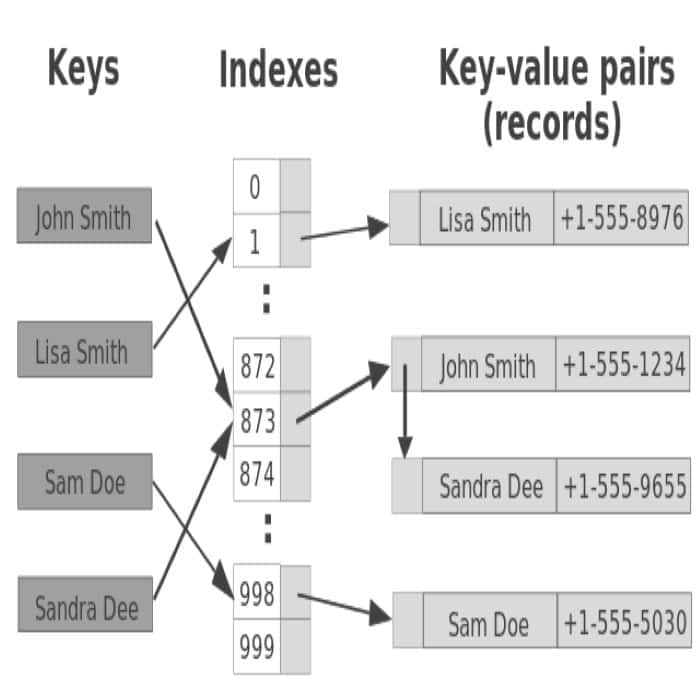
We can implement a hash table by usingĪ list with each element initialized to the special Python value None. For example, we will have a slot named 0, a slot Often called a slot, can hold an item and is named by an integer We will see, however, that this isĪ hash table is a collection of items which are stored in such a wayĪs to make it easy to find them later. Item is where it should be, then the search can use a single comparison Items might be when we go to look for them in the collection. In order to do this, we will need to know even more about where the In this section we will attempt to go one stepįurther by building a data structure that can be searched in O ( 1 ) O(1) O ( 1 ) Knowing that a list was ordered, we could search in logarithmic time Stored in the collection with respect to one another. In previous sections we were able to make improvements in our searchĪlgorithms by taking advantage of information about where items are


 0 kommentar(er)
0 kommentar(er)
